(Перед вами перевод бесплатного курса по A/B тестированию от компании Dynamic Yield. Если вы здесь впервые, то лучше начните сначала)
Авторы английской версии: Дэвид Стейнберг, профессор, KPA Group; Рон Кенет, профессор, KPA Group
A/B тестирование — это отличный способ сравнения нескольких возможных модификаций сайта или несколько альтернативных опытов взаимодействия с цифровым продуктом/сервисом. Мы запускаем две вариации визуала/опыта параллельно и случайным образом распределяем посетителей между ними — в результате чего получаем честное сравнение эффективности этих вариаций.
Получить данные тестирования мало — вам понадобятся надежные и информативные способы обобщить эти данные и сделать правильные выводы. Байесовский подход к статистике отлично справляется с этой задачей.
В этой статье мы поговорим о ключевых идеях, которые лежат в основе байесовской статистики, и о том, как они соотносятся с бизнес-решениями, которые мы принимаем по итогам тестирования.
Сначала мы продемонстрируем суть байесовского подхода к анализу данных, а потом покажем, как анализ данных помогает находить понятные ответы на подобные вопросы:
- Какая вариация обеспечивает лучшие результаты?
- Насколько эти результаты лучше?
- Можем ли мы быть уверены в своих выводах?
- Что если нужно протестировать более двух вариаций?
- Какой объем выборки нужен для проведения байесовского A/B теста?
- Можно ли закончить тест раньше, если результаты кажутся очевидными?
Что такое байесовская статистика?
Байесовская статистика носит имя британского математика и священника Томаса Байеса, жившего в 18 веке и доказавшего частный случай теоремы, сейчас называемой теоремой Байеса. Ключевой принцип байесовской статистики состоит в том, что язык вероятностей можно использовать для описания любых вещей и явлений, о которых мы ничего не знаем и хотим узнать из данных.
Сейчас мы продемонстрируем почему это идеальный язык для обсуждения важных вопросов, связанных с принятием ключевых бизнес-решений.
Когда вы проводите A/B тест, ваша основная цель — выяснить, какая из вариаций работает эффективнее. Чтобы это понять, вы можете сравнить результаты тестирования, используя один из двух методов (частотный или байесовский). Байесовский анализ начинается с изучения KPI каждой вариации. Данные дают нам определенную информацию об эффективности вариаций, но некоторая неопределенность всегда остается. Эту неопределенность мы описываем через распределение вероятностей. Мы можем смоделировать результаты распределения, чтобы понять, как это выглядит.
Гистограмма на рисунке 1 — это типичная картина, которую вы можете получить в ходе анализа. Она показывает статистическое распределение разницы в CTR (click-through rate) между A и B. Большая часть кривой находится справа от 0, что является доказательством того, что у A показатель CTR выше. Часть графика, лежащая по правую сторону от 0 является отличной иллюстрацией того, что называется Probability to Be Best (P2BB) — вероятность того, что одна опция лучше другой. На рисунке 1, показатель P2BB составляет 0,699 — в пользу вариации А.
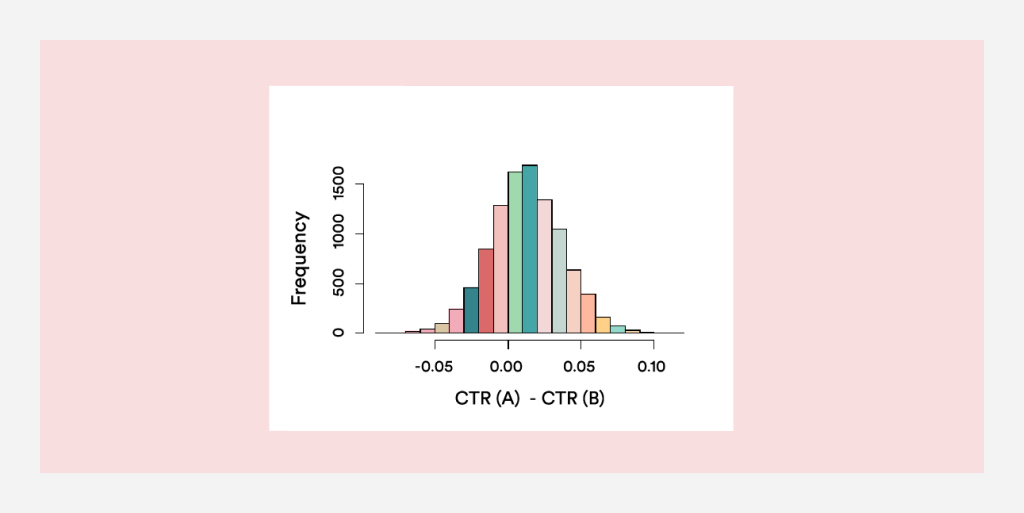
Если у вас три или более вариаций, высчитать вероятность того, что каждая опция лучше остальных (P2BB) тоже просто: вероятность в этом случае будет поделена на 3 части части — по одной для каждого варианта.
Как работает байесовский анализ?
Чтобы запустить байесовский движок, вам потребуется априорное распределение вероятностей, которое описывает ваше представление о KPI до получения каких-либо данных. Далее это априорное распределение комбинируется с данными теста, в результате чего получается апостериорное распределение для каждой вариации. То есть на рисунке 1 мы видим апостериорное распределение вероятностей для разницы между вариациями A и B — оно иллюстрирует текущую картину, основанную на полученных данных.
Априорное распределение нужно, чтобы процесс заработал, но при большом объеме данных — который присутствует почти всегда в A/B тестах — апостериорное распределение сразу начинает доминировать и априорное распределение практически “забывается”; поэтому не нужно слишком заморачиваться с выбором априорных показателей. Можно работать с более-менее стандартными показателями — на качество анализа это не повлияет.
Но можно ли заранее обозначить априорное распределение и сделать какие-то предположения? Долгое время это было камнем преткновения между представителями двух статистических лагерей, поэтому давайте сравним байесовский подход с “классическим” частотным подходом, который вы скорее всего изучали в рамках вводного курса по статистике. В классическом подходе, либо А лучше B, либо B лучше А, либо А и B идентичны. Вопрос “какова вероятность, что B лучше” вообще не стоит: ответить на него нельзя, более того, и сам вопрос нельзя задавать!
Вероятности используются и в классическом подходе — но только для описания экспериментальных данных, а не для обобщения информации, которой мы располагаем по KPI. Поэтому вы не сможете сделать выводы типа “В покажет лучшие результаты, чем A с вероятностью 98%”.
В большинстве A/B тестов вы будете получать огромные объемы данных. Таким образом, априорные предположения, которые мы делаем на старте — даже если они в какой-то мере противоречивы, быстро перекроются реальными данными, которые и лягут в основу будущих результатов. Поэтому мы считаем, что выводы сделанные в ходе байесовского анализа больше подходят для принятия бизнес-решений.
В этой статье можно прочитать про разные точки зрения относительно сравнения байесовского и частотного подходов к A/B тестированию.
Как распределять трафик между вариациями?
По большому счету, вам важно убедиться, что посетители, которые увидят вариацию A максимально схожи с посетителями, которые увидят вариацию B. Лучший способ в этом убедиться (согласно научным работам, в том числе работам статистика Рональда Фишера 100-летней давности) — это выбор правильного распределения трафика.
Так что в первую очередь надо прикинуть, какие у вас вводные. Что вы хотите сравнить? Вам понадобится механизм распределения трафика — фреймворк, который будет определять, что кому показывать.
Когда посетитель приходит на ваш сайт, обычно он сразу видит некий лендинг. Но когда вы проводите тестирование, вам нужно сначала решить, на какую версию лендинга направлять того или иного пользователя. Вы можете (и должны) это контролировать, случайным образом распределяя посетителей по группа. Только так можно быть уверенным, что сравнение будет честным.
Чтобы проверить релевантность данных, которые вы получаете в ходе тестирования, нужно убедиться, что распределение трафика действительно происходит случайным образом.
К примеру, если версия А показывается молодым людям, а версия B — людям в возрасте, вы никак не узнаете, чем объясняется разница в KPI: дизайном страницы или спецификой восприятия пользователями разного возраста. В статистике это называется “вмешивающимся факторов” (confounding).
Таким образом, случайное распределение трафика позволяет установить некоторую причинно-следственную связь между поведением пользователей и тем, что влияет на это поведение.
Сколько времени нужно выделить на проведение A/B теста?
Принимая решения, вы должны учитывать разные возможные сценарии — и в том числе “что может пойти не так”. Нужно, чтобы тест был чувствительным к возможным багам. Баги, в свою очередь, часто бывают связаны именно со случайным распределением посетителей в контексте времени. В частности, естественные временные тренды могут значительно повлиять на результаты тестирования.
Например, если в ваших есть недельные тренды, нужно проводить A/B тестирование как минимум на протяжении двух недель, чтобы убедиться, что механизм тестирования успешно их обрабатывает. Если у вас есть суточные тренды (не недельные), вы можете позволить себе более краткосрочные эксперименты. Также бывают ситуации, когда из-за определенных событий случаются спонтанные скачки трафика (как в плюс, так и в минус) или меняется состав посетителей, что влияет на KPI. Прежде чем принимать какие-либо решения, убедитесь, что на результаты не повлияло то или иное эпизодическое событие.
Если вы примете во внимание все факторы, изложенные выше, то сможете точно прикинуть минимальную продолжительность эксперимента, при которой каждая из групп при A/B тестировании будет репрезентативной.
Насколько большая выборка нужна для проведения байесовского тестирования?
Размер выборки при байесовском тестировании напрямую влияет на то, насколько узкой будет ваша финальная функция распределения вероятности. Допустим, вам нужна функция распределения вероятности, чтобы выявить разницу в эффективности двух вариаций, как показано на рис. 1. Скорее всего, вы уже примерно представляете, какая разница будет существенна для вашего бизнеса — и, следовательно, вы понимаете, насколько узкой должны быть финальная функция вероятности: ведь чем плотнее интервал — тем больше вы знаете.
Также важно отметить, что если люди, принявшие участие в тестировании, принадлежат к какой-то одной подгруппе пользователей (даже если они были случайно отобраны таким образом), то результаты такого тестирования нельзя экстраполировать на всех пользователей — какой бы плотной ни была при этом функция распределения. Так что вам нужно работать по обоим направлениям: во-первых, убедиться, что у вас достаточно данных, чтобы функция распределения получилась плотной (следовательно более информативной), а во-вторых — оценить, насколько репрезентативны ваши данные относительно всей совокупности пользователей.
Оба эти аспекта важны, и именно они определяют, насколько масштабным будет ваш эксперимент. Скажем, если на вашем сайте огромный трафик, вы быстро достигнете нужного объема выборки, но насколько репрезентативной будет эта выборка — сказать сложно. Может сложиться и обратная ситуация: к тому времени, как выборка достигнет нужного объема, вы пройдете несколько временных циклов — и, следовательно, охватите и обработаете возможные эпизодические скачки трафика. Держите в голове оба эти “направления” и постоянно ищите баланс между ними.
Где взять информацию о наиболее вероятных значениях KPI? Если одна из ваших вариаций уже работает на сайте, можно взять данные за прошлые периоды для составления априорного распределения. Если обе вариации новые, вам нужно прикинуть, какой эффект они могут оказать на KPI? Для тестов, в которых участвуют более двух вариаций, работает тот же принцип и нужны те же данные.
Входные данные, необходимые для расчета нужного объема выборки, зависят от природы ваших KPI:
- Для бинарных KPI (коэффициент кликабельности (CTR) или доля установок), укажите ожидаемые значения этих показателей для каждой версии
- Если вас интересуют только непрерывные KPI (например, доход с конверсии), вам потребуется указать типичные средние конверсии и количество участников в каждой экспериментальной группе
- Для смешанных KPI (например, доход с пользователя) вам потребуется среднее, количество вариантов, а также оценка доли успешных конверсий
Есть достаточно простые формулы, которые можно использовать для определения объема выборки. Кроме того, здорово помогают калькуляторы объема выборки для A/B тестов
Что если у меня более двух вариаций в тестировании?
В ситуации, когда вы хотите протестировать более двух вариаций, применимы те же формулы для вычисления нужного объема выборки. Но в этом случае важно определиться, какую цель мы преследуем: (1) выявить лучшую вариацию или (2) показать, что текущая вариацию не лучшая.
Чем отличается вторая цель?
Допустим у вас есть две новые вариации, которые вы хотите сравнить с текущей. Вы предполагаете, что каждая из новых вариаций может показать примерно одинаковые KPI, и при этом обе будут эффективнее, чем текущая версия. В этом случае, чтобы выяснить какая из этих новых версий лучше, вам понадобится довольно большой объем выборки (поскольку версии схожи по эффективности). А просто “списать” текущую версию в пользу одной из новых можно при помощи куда менее масштабного теста.
Рассмотрим на примере:
CTR текущей страницы составляет 1%. Вы уверены, что новая версия поможет увеличить CTR до 1,2%. Предполагаемая разница в KPI — 0,2%. Вы решаете провести A/B тест, чтобы выявить истинную разницу с более высокой степенью чувствительности. В этом случае мы стремимся к такой чувствительности эксперимента, при которой 95% апостериорного распределения будет находиться в интервале, который равен величине предполагаемой разницы.
В нашем примере это означает, что мы будем сужать функцию распределения, пока 95% этой функции не станут находиться в интервале 0,002. Чтобы добиться такой точности, нам нужна выборка в 83 575 посетителей на каждой странице.
А что если даже 10%-ное увеличение CTR (то есть до 1,1%) является значительным? Тогда интервал, в котором должно находиться 95% функции распределения сужается еще сильнее — до 0,1%. В этом случае каждую страницу должны посетить не менее 319 290 человек.
Теперь давайте рассмотрим пример того, как оценить доход на посетителя:
Чаще всего львиная доля посетителей сайта вообще не приносят никакого дохода (согласно принципу Парето), а среди тех посетителей, кто платит, как правило есть несколько крупных игроков, чьи чеки искажают среднее значение, а также стандартное отклонение. Итак, на текущей версии страницы конверсия составляет 1%; в среднем сконвертированный посетитель приносит 20$; стандартное отклонение по сумме покупки составляет 25$. Это означает, что средний доход на посетителя составляет 0,20$. Команда маркетинга уверена, что с новой версии страницы будут покупать чаще, и конверсия увеличится до 1,2%, но доля крупных игроков уменьшится — так что средняя конверсия будет приносить 19$, а стандартное отклонение уменьшится до 22$.
В результате средний доход с конверсии вырастет до 0,228$ — то есть ожидается рост в 0.028$ на посетителя. A/B тест должен быть достаточно масштабным, чтобы сузить 95%-ный доверительный интервал, характеризующий разницы в среднем доходе с посетителя, до предполагаемой разницы — то есть 0,028$. Чтобы добиться такого уровня точности, нам нужно привлечь не менее 397,830 посетителей на каждую вариацию страницы.
Что если нам нужны более надежные гарантии, что мы выявим значительную разницу?
В самом начале мы обозначили, что подбираем размер выборки таким образом, чтобы добиться нужной нам ширины 95%-ного доверительного интервала. Повысить надежность эксперимента просто: достаточно расширить границы доверительного интервала до 98 или 99%. Конечно, дополнительная точность достигается ценой увеличения объема выборки.
Можно ли завершить тест пораньше?
Вероятность, что вариация A лучше (или хуже) вариации B — это естественная метрика, которую можно отслеживать по мере проведения тестирования. Если показатель P2BB (вероятность, что одна вариация лучше другой) явно сигнализирует о том, что одна из версий эффективнее, это может быть поводом для ранней остановки эксперимента. Однако, останавливать эксперимент раньше времени нужно с умом.
Во-первых, нельзя с уверенностью утверждать, что байесовские выводы не подвержены проблеме подглядывания. В ходе эксперимента показатель P2BB так или иначе будет плавать. Особенно это относится к тем случаям, когда нет значительной разницы в итоговых показателях вариаций — например, при A/A тестировании. В этом случае, по мере того как в эксперименте задействуется все больше данных, P2BB будет то повышаться, то снижаться. То, что в какой-то момент времени показатель P2BB превысит пороговое значение в 95%, совсем не гарантирует, что он останется на том же уровне и дальше — в рамках запланированного временного интервала.
Во-вторых, остановка эксперимента до того, как пройдет как минимум один полный временной цикл, это всегда риск. Вариация B, может оказаться более удачной для тех людей, кто зашел на сайт в начале временного цикла, но менее удачной для более поздних посетителей. Следовательно, останавливая эксперимент до того завершения полного временного цикла, вы рискуете получить искаженные данные.
Если вы очень хотите остановить эксперимент раньше, продумайте более строгие критерии, достижение которых вас устроит. К примеру, если вы видите, что вероятность достигает предельных значений (например, выше 0.999 или ниже 0.001), можете смело останавливать эксперимент и принимать решение. Если вариации A и B действительно значительно отличаются, можно ожидать, что эти пороговые значения будут достигнуты относительно быстро.
И наконец, хочется еще раз подчеркнуть, как важно охватить все временные тренды в рамках эксперимента. Конечно, вы можете принять решение основываясь на показателях короткого временного окна — но, поступая так, вы игнорируете возможные колебания результатов, которые могут проявиться позже. Например, бывает так, что посетители, которые заходят на сайт по будням, предпочитают вариацию A, но в выходные картина полностью меняется. Условно говоря, начать эксперимент во вторник, а в среду уже принимать решение — не лучшая идея.
← Назад | Продолжение (Глава 9) →






